
DeeP MeLT
Arson's Lab
Mechanics of fragmentation
Experimental mechanics and Discrete Element Method
Particulate fragmentation, the process by which large particles break into fragments, results in important changes Particle Size Distribution (PSD), particle shape, void ratio, permeability, compressibility, shear strength and stress-strain behavior. Particulate breakage can occur in different geomaterials from crushable granular materials to rock-fills and concrete aggregates. Various constitutive laws were proposed to relate the mechanical behavior of granular materials to breakage indexes. Despite the progress made on modeling granular mechanics at the macro-scale, discriminating the mechanisms that control particle breakage within a particulate assembly is still an open issue. For example, particle strength is known to decrease with particle size (so called size effect). But statistically, larger particles are more likely to have a larger coordination number, thus to be subjected to a more uniform contact stress (so called shielding effect) and to have a lower probability of breakage. As a result, the conditions in which a large particle size prevents breakage are not well understood. Here, we analyze particle fragmentation and the associated energy distribution from a micro-mechanical standpoint.
- P. Wang, N. Gao, K. Ji, L. Stewart, C. Arson, 2020. DEM analysis on the role of aggregates on concrete strength, Computers and Geotechnics, DOI:10.1016/j.compgeo.2019.103290.
- P. Wang, Z. Karatza, C. Arson, 2019. DEM Modelling of sequential fragmentation of zeolite granules under oedometric compression based on XCT observations, Powder Technology, DOI: 10.1016/j.powtec.2019.02.050.
- P. Wang, C. Arson, 2018. Energy distribution during the quasi-static confined comminution of granular materials, Acta Geotechnica, DOI: 10.1007/s11440-017-0622-5.
- P. Wang, C. Arson, 2016. Discrete Element Modeling of shielding and size effects during single particle crushing, Computers and Geotechnics, DOI: 10.1016/j.compgeo.2016.04.003.
Sequential fragmentation
We analyzed micro-CT scans obtained sequentially during an oedometer test of zeolite to model crushing at the scale of a granular assembly. We implemented a new breakage model in DEM, which combines particle replacement, for primary splitting breakage, and cluster bond breakage, for modeling fragment breakage. An important improvement upon previously published models is that during tensile splitting, the breakage plane is defined by the contact carrying the maximum normal force and direction of minimum principal stress, instead of assuming that the breakage plane contains the two maximum contact force vectors. The PSD obtained with the new DEM model exhibits an impressive matching with experimental results. Additionally, the new breakage model can capture the experimental stress-strain relationship at the macroscopic scale.
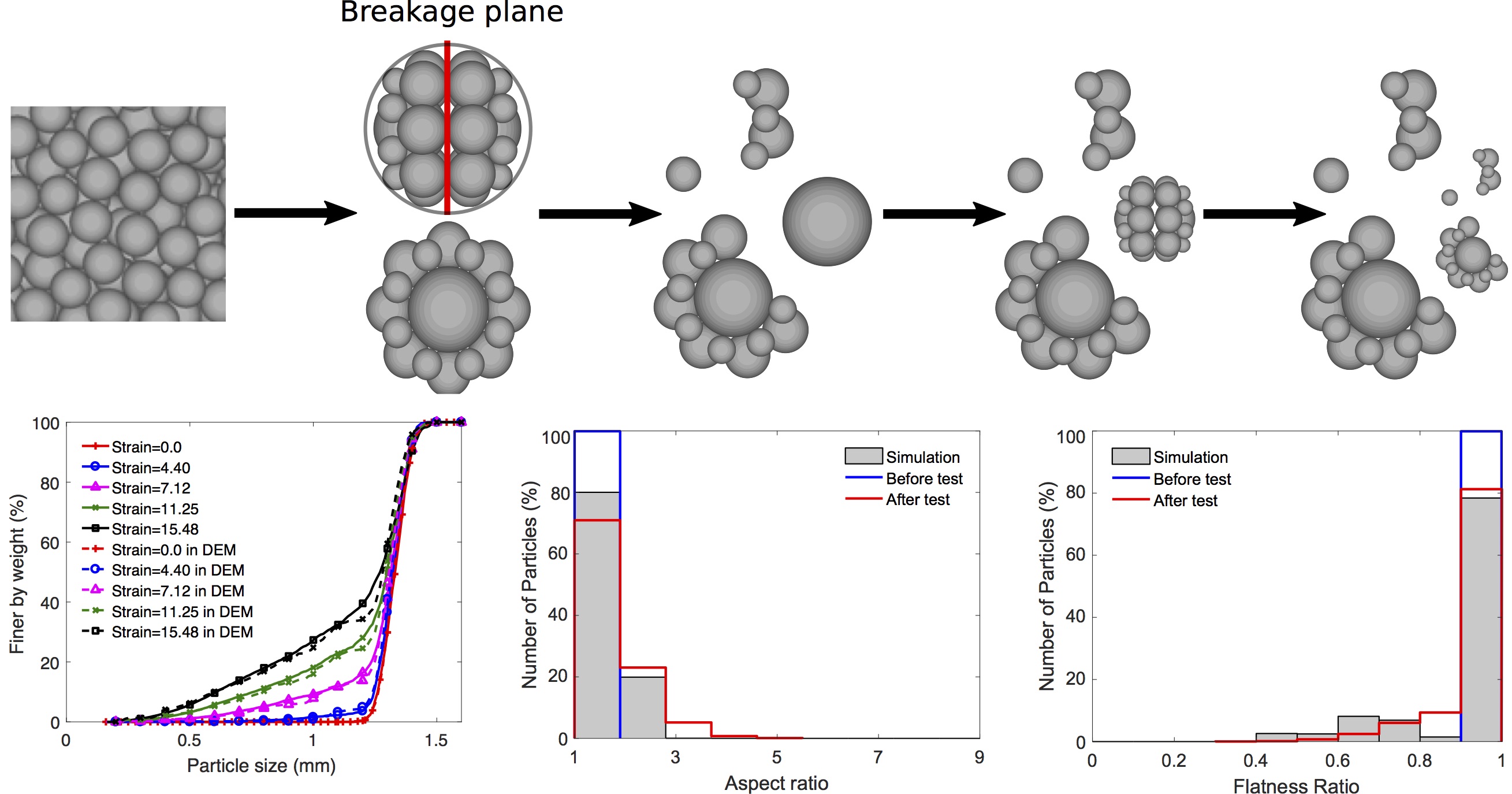
Pictures: Wang, Karatza and Arson, 2019
Energy dissipation during comminution
We analyzed the evolution of the energy of a granular assembly subject to particulate breakage during quasi-static confined comminution. Energy potentials are related to internal variables that have a clear relationship to microstructure evolution, e.g. deviation to initial and ultimate PSDs, particle specific surface, porosity. DEM simulations show that: At least 60% of the work input is dissipated by particle redistribution; The fraction of elastic deformation energy increases and the fraction of redistribution energy decreases as the compression stress increases; The breakage energy accounts for less than 5% of the total input energy, and this value is independent of the compressive stress; The energy dissipated by redistribution is between 14 to 30 times larger than the breakage energy.
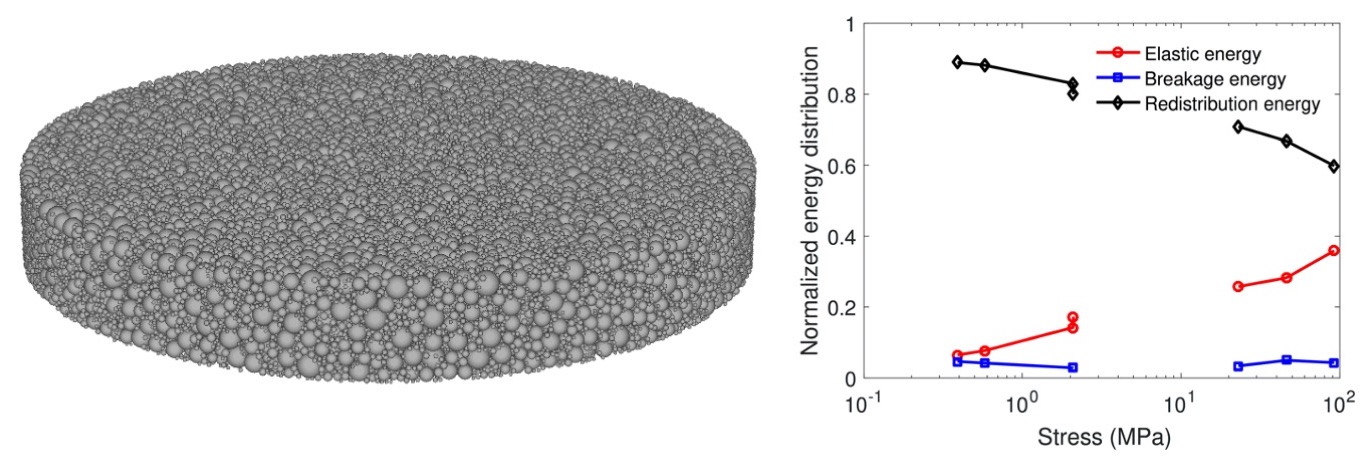
Pictures: Wang and Arson, 2018
Shielding vs. Size Effects
A DEM model of crushable particle was designed and calibrated against experimental results of uniaxial compression tests on single sand grains. The calibrated model was then used to study the influence of the coordination number on the peak force at initial failure ("shielding effects"). We conducted a sensitivity analysis to understand in which conditions shielding effects overcome size effects. We also investigated the influence of microscopic flaws on particle crushing. Our simulations highlight the predominant influence of porosity over flaw size and show that particle strength depends linearly on the particle coordination number and quadratically on particle porosity.
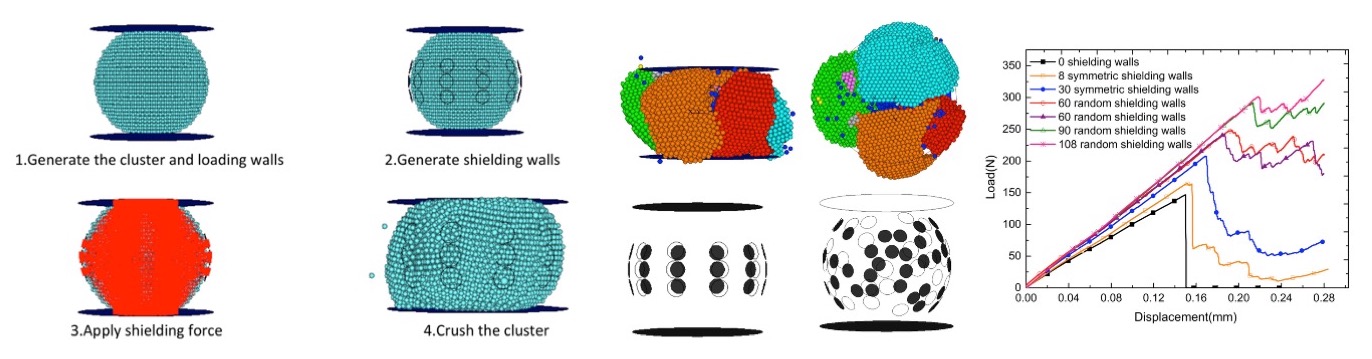
Pictures: Wang and Arson, 2016
Fragmentation in bonded aggregates
We proposed a DEM displacement-softening contact model to simulate fracture propagation in concrete. Aggregate contours are imported from point clouds obtained by scanning actual aggregates. The Interfacial Transition Zone (ITZ) is accounted for by deleting bonds at the interface between aggregates and mortar. The model was calibrated against results of uniaxial compression tests and Brazilian tests of both mortar and concrete. DEM simulations confirm that concrete does not fail in pure tensile mode during Brazilian tests. Sensitivity analyses also show that concrete strength depends linearly on both the adhesive area fraction of the ITZ and the aggregate tensile strength. The ITZ has a greater effect on concrete strength than aggregate strength.
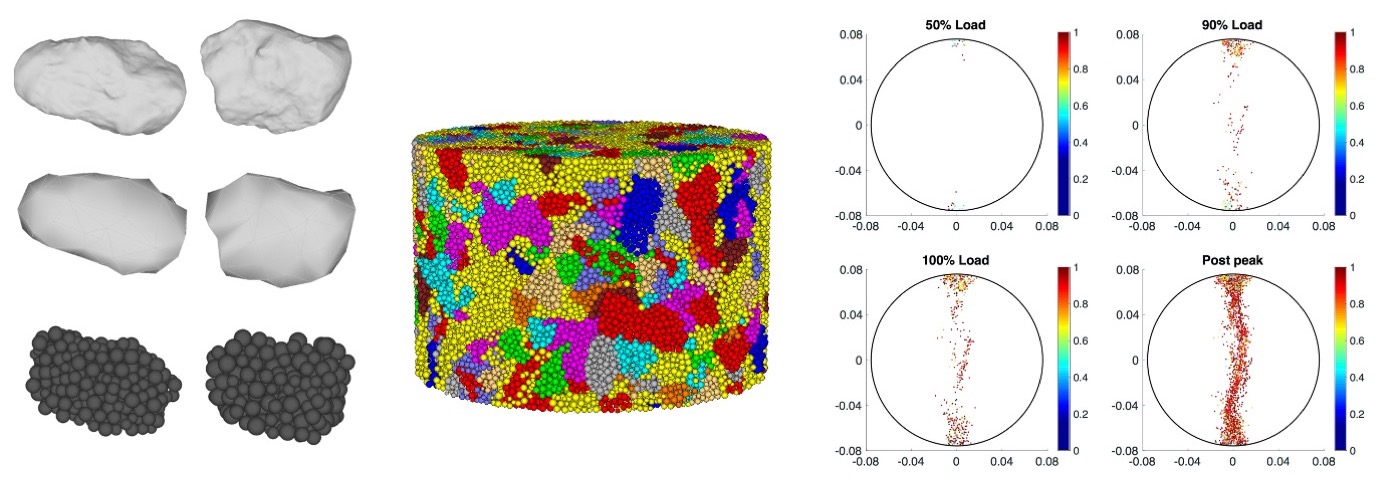
Pictures: Wang, Gao, Ji, Stewart and Arson, 2020