
DeeP MeLT
Arson's Lab
Micro-macro modeling of damage and healing in rocks
Homogenization theory, micromechanics, fabric enrichment
Damage and healing rock mechanics is important to design safe underground storage facilities, assess the impact of hydraulic fracturing, understand fault dynamics and simulate geomorphological processes. Historically, engineers have used phenomenological models that cannot explain all the complex crack patterns observed in the field or predict accurately damaged rock properties in the long term. To overcome these limitations, we formulated novel micro-macro models of crack initiation, opening, closure and rebonding for carbonate rock, granite and halite, which are common geological host materials. Based on micro-mechanics and homogenization principles, the proposed models do not only explain the mechanical behavior of damaged rocks with intrinsic anisotropy, but can also be used to assess natural geological substrates or design engineered geomaterials for optimal drilling or storage operations.
- T. Xu, C. Arson, 2023. Interface homogenization approach for mechanical healing driven by pressure solution, Journal of Engineering Mechanics (accepted)
- T. Xu, X. Shen, M. Reed, N. West, K.L. Ferrier, C. Arson, 2022. Anisotropy and microcrack propagation induced by weathering, regional stresses and topographic stresses, Journal of Geophysical Research - Solid Earth, DOI: 10.1029/2022JB024518
- Z. Wu, T. Xu, C. Arson, 2022. Effect of the intermediate principal stress on pre-peak damage propagation in hard rock under true triaxial compression, Rock Mechanics and Rock Engineering, DOI: 10.1007/s00603-022-02981-x
- T. Xu, C. Arson, 2022. Self-consistent approach for modeling coupled elastic and visco-plastic processes induced by dislocation and pressure solution, International Journal of Solids and Structures, DOI: 10.1016/j.ijsolstr.2021.111376
- J. Ding, F.M. Chester, J.S. Chester, X. Shen, C. Arson, 2021. Coupled brittle and viscous micromechanisms produce semibrittle flow, grain-boundary sliding, and anelasticity in salt-rock, Journal of Geophysical Research: Solid Earth, DOI: 10.1029/2020JB021261
- X. Shen, J. Ding, I. Lordkipanidze, C. Arson, J. Chester, F.M. Chester, 2021. Fabric evolution and crack propagation in salt during consolidation and cyclic compression tests, Acta Geotechnica, DOI: 10.1007/s11440-020-01117-1.
- X. Shen, J. Ding, C. Arson, F. Chester, J. Chester, 2021. Micro-mechanical Modeling for Rate-Dependent Behavior of Salt Rock under Cyclic Loading, International Journal for Numerical and Analytical Methods in Geomechanics, DOI: 10.1002/nag.3133.
- X. Shen, C. Arson, J. Ding, F. Chester, J. Chester, 2020. Mechanisms of anisotropy in salt rock upon micro-crack propagation, Rock Mechanics and Rock Engineering, DOI : 10.1007/s00603-020-02096-1.
- C. Arson, 2020. Micro-macro mechanics of damage and healing in rocks, Open Geomechanics, DOI: 10.5802/ogeo.4.
- X. Shen, C. Arson, K. Ferrier, N. West, S. Dai, 2019. Mineral weathering and bedrock weakening: Modeling microscale bedrock damage under biotite weathering, Journal of Geophysical Research: Earth Surface, DOI:10.1029/2019JF005068.
- X. Shen, C. Arson, 2019. An isotropic self-consistent homogenization scheme for chemomechanical healing driven by pressure solution in halite, International Journal of Solids and Structures, DOI: 10.1016/j.ijsolstr.2018.11.010
- A. Pouya, C. Zhu, C. Arson, 2019. Self-consistent micromechanical approach for damage accommodation in rock-like polycrystalline materials, International Journal of Damage Mechanics, DOI: 10.1177/1056789517747665
- W. Jin, C. Arson, 2018. Anisotropic nonlocal damage model for materials with intrinsic transverse isotropy, International Journal of Solids and Structures, DOI: 10.1016/j.ijsolstr.2018.01.020.
- W. Jin, C. Arson, 2018. Nonlocal enrichment of a micromechanical damage model with tensile softening: advantages and limitations, Computers and Geotechnics, DOI: 10.1016/j.compgeo.2017.09.011.
- W. Jin, C. Arson, 2017. Discrete Wing Crack based Damage Model for Brittle Solids, International Journal of Solids and Structures, DOI:10.1016/j.ijsolstr.2016.12.025
- S. Le Pense, C. Arson, A. Pouya, 2016. A fully coupled damage-plasticity model for unsaturated geomaterials accounting for the ductile - brittle transition in drying clayey rocks, International Journal of Solids and Structures, DOI: 10.1016/j.ijsolstr.2016.04.007.
- A. Pouya, C. Zhu, C. Arson, 2016. Micro-Macro Approach of Salt Viscous Fatigue under Cyclic Loading, Mechanics of Materials, DOI: 10.1016/j.mechmat.2015.10.009.
- C. Arson, T. Vanorio, 2015. Chemo-mechanical evolution of pore space in carbonate microstructures upon dissolution: linking pore geometry to bulk elasticity, Journal of Geophysical Research: Solid Earth, DOI: 10.1002/2015JB012087.
- C. Zhu, C. Arson, 2015. A model of damage and healing coupling halite thermomechanical behavior to microstructure evolution, Geotechnical and Geological Engineering, DOI: 10.1007/s10706-014-9797-9.
- C. Arson, Z. Medina-Cetina, 2015. Bayesian Paradigm to Assess Rock Compression Damage Models, Environmental Geotechnics, DOI: 10.1680/envgeo.13.00039.
Homogenization scheme for pressure-solution driven healing
Pressure solution is a very effective healing mechanism, common in crystalline media. A chemomechanical homogenization model was formulated to predict the long term healing process in geomaterials. The inclusion is a hollow sphere that contains a spherical void located at the intersection of three orthogonal grain-to-grain contact planes. Pressure solution induces geometric changes, which are used to calculate the viscous strain rate of the inclusion. Sensitivity analyses at the inclusion scale indicate that the healing rate is maximum when one of the contact planes is orthogonal to the compressive loading direction. Hill's inclusion-matrix interaction law is used to upscale strains and stresses at the scale of a Representative Elementary Volume (REV). Oedometer tests are simulated for specimens containing spherical inclusions with uniformly distributed contact plane orientations. It is observed that in samples with same porosity but with inclusions that have different initial void sizes, inclusions with larger voids have a negligible healing rate and they are slowing down the overall healing rate of the REV. The highest healing rate is reached in samples with uniformly distributed void sizes. In addition, the healing rate increases with the initial porosity, but the final porosity change does not depend on the initial porosity of the sample. Principal stresses of higher magnitude are noted in the inclusions that are part of REVs of high initial porosity. In specimens with smaller inclusions (i.e., smaller grains), principal stresses are more widely distributed in magnitude and the healing rate is higher.
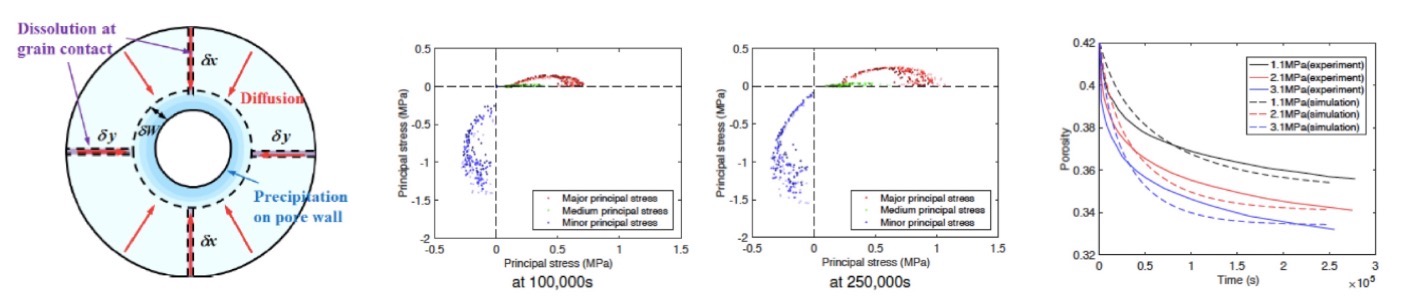
Pictures: Shen and Arson, 2019
Homogenization scheme for granite chemical weathering
We formulated a micro-macro chemo-mechanical model in which biotite minerals are represented by oblate spheroidal inclusions embeded in a homogeneous matrix that represents the other minerals that compose the granite rock under study. The homogenization scheme is based in Eshelby's theory and the chemically-driven expansion of biotite is modeled as an eigenstrain. The matrix is assigned a damage-elastic constitutive law, which allows prediction of the initiation of micro-fractures with a length of the same order of magnitude as that of biotite minerals. Sensitivity analyses show that biotite weathering can indeed induce micro-fracture propagation in granite. It is found that the higher the biotite volume fraction, or the smaller the biotite aspect ratio, the earlier the initiation of matrix damage and the larger the REV volumetric strain. When the REV is constrained horizontally by fixed displacements, a smaller angle between thickness direction and horizontal direction leads to greater damage in the matrix.
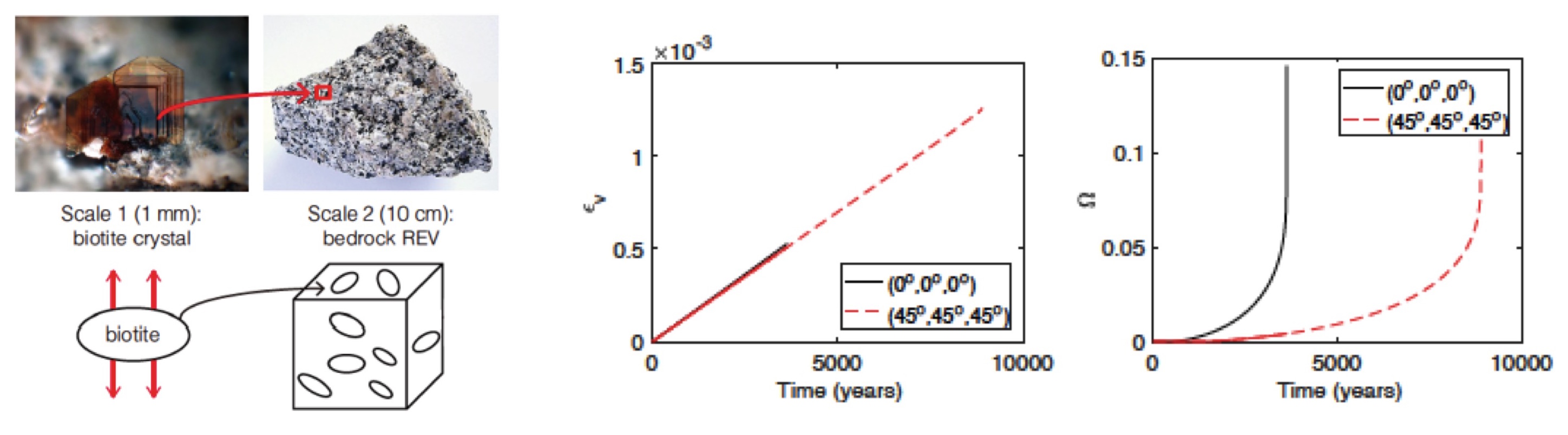
Pictures: Shen, Arson, Ferrier, West and Dai, 2019
Homogenization scheme for salt rock viscous damage
Underground cavities in salt rock formations used for Compressed Air Energy Storage (CAES) undergo cyclic loads and are subject to a fatigue phenomenon that induces a decrease of rock strength and stiffness. A micromechanical analysis of this phenomenon is necessary to understand its mechanisms and elaborate relevant constitutive models. The goal of this research project is to model the macroscopic damage induced by the breakage of grains that undergo microscopic stresses that exceed halite tensile strength. The polycrystalline nature of rock salt has a crucial effect on crack propagation and rock damage and, hence, on fatigue behavior. This behavior was investigated on the basis of self consistent upscaling approaches for viscous heterogeneous materials. The internal stresses in the polycrystal were modeled based on experimental data available for halite single crystals. The simulation of monotonic compression tests allowed tracking the triggering of fatigue damage. Results showed that tensile stresses are developed in the polycrystal under global compressive load, the amplitude of which depends on the macroscopic load rate or frequency. The figures below show that higher microstresses develop when the specimen is subjected to a higher number of loading cycles.
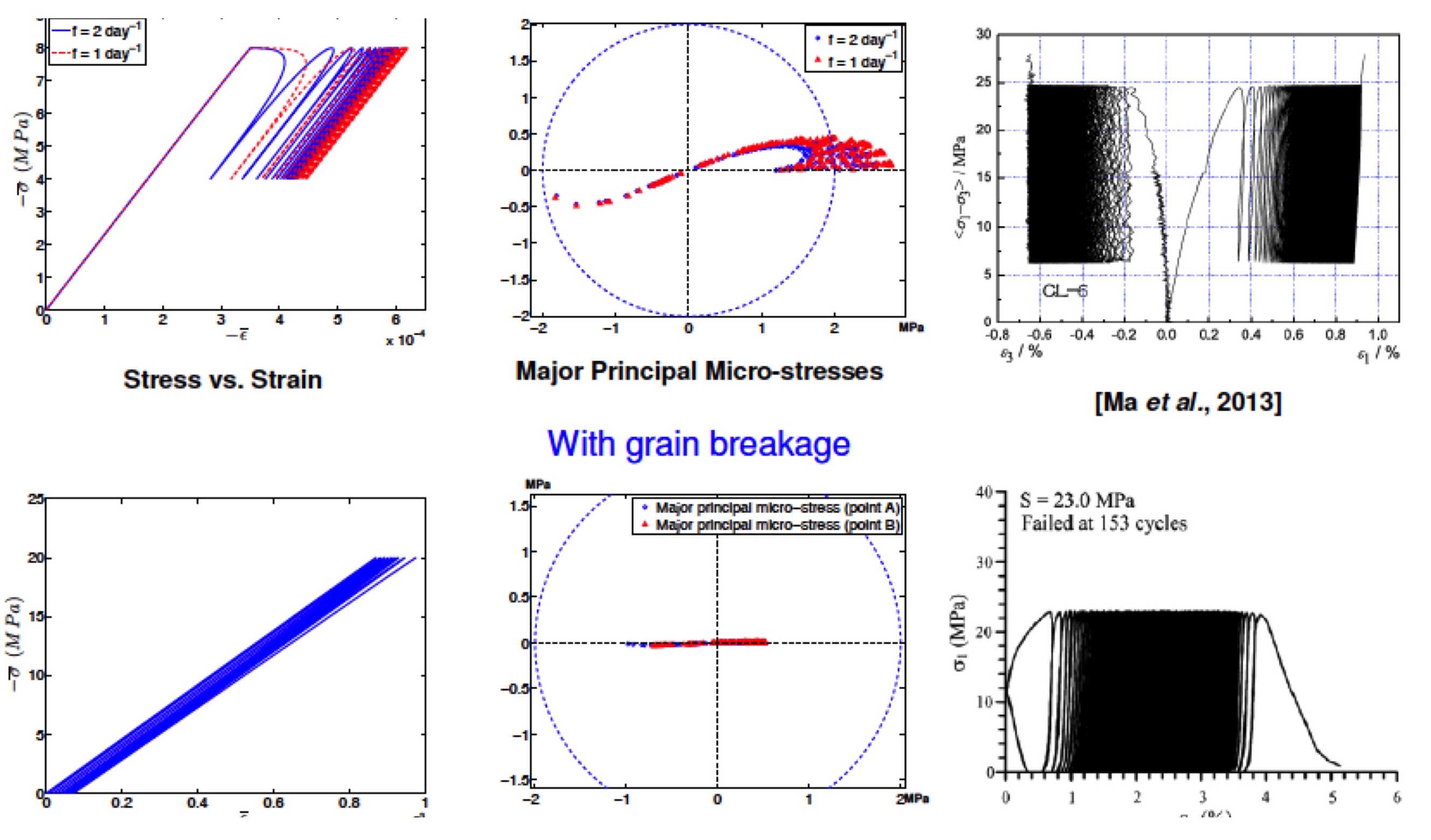
Pictures: Zhu, Pouya and Arson, 2015
Mixed mode anisotropic micro-crack propagation
Two novel anisotropic damage models were formulated to explicitly account for the evolution of discrete sets of micro-cracks. Both models are based on the same free enthalpy expression, derived from a dilute homogenization scheme, using 42 sets of crack families of different orientations. These two models differ by their damage criteria and crack evolution laws: the first model is based on the theory of wing crack development, whereas the second model is based on a radial crack growth law, which depends on a phenomenological driving force. The phenomenological model is implemented into Abaqus User MATerial (UMAT) subroutines, and a return-mapping algorithm (closest point projection) is used to ensure that the state variables remain on the multiple activated yield surfaces. Results of material point and finite element simulations demonstrate that the models capture inelastic deformation, unilateral effects and distinct strength and stiffness properties in tension and compression, for complex stress paths involving the propagation of both open and closed cracks in mixed mode.
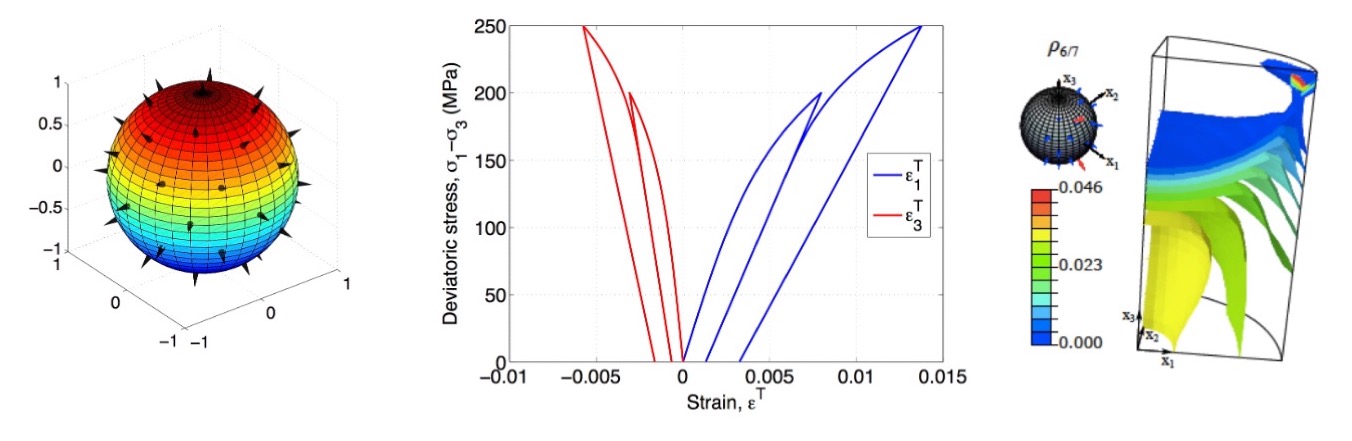
Pictures: Jin and Arson, 2017
Fabric-enriched damage mechanics
Uniaxial consolidation test were conducted on reagent-grade granular salt in dry conditions at 150 C. 2D-microscopic images, parallel to the axis of consolidation, were obtained at several stages of progressive consolidation from 15% to 3% porosity. Microstructure image analyses were performed to obtain probability density functions (PDFs) of the area, solidity, coordination number, orientation, elongation and roundness of the grains, as well as the PDFs of the branch lengths, branch orientations and solid volume fraction, defined locally over polygons with edges matching grain centroids. It is found that sample deformation is mostly due to grain rearrangement and that upon consolidation, grains become less convex, and elongate in the direction perpendicular to the loading axis. Four fabric tensors were calculated to assess microstructure anisotropy induced by grain orientation, branch length orientation, grain solidity and local solid volume fraction. Fabric tensors were diagonal and orthogonal, therefore their product was used to define a global fabric tensor, which was introduced in the expression of the stiffness tensors. The constitutive parameters were calibrated against the consolidation tests. The approach paves the way to enrich continuum damage and healing mechanics model with fabric descriptors that can play the role of internal variables.
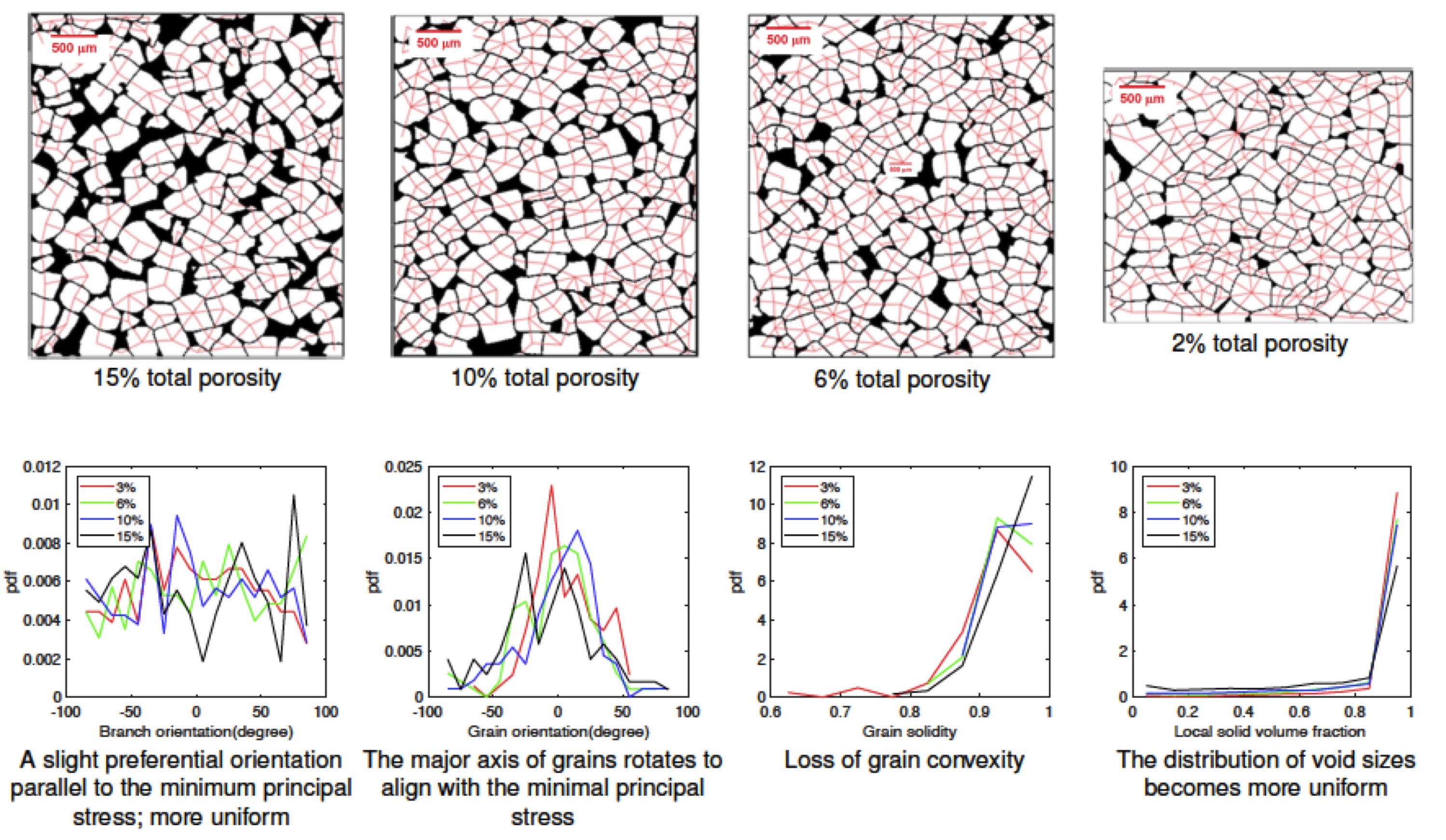
Pictures: Shen and Arson, 2017
Microstructure-enriched model of damage and healing
Creep processes in halite (salt rock) include glide, cross-slip, diffusion and dynamic recrystallization. Diffusive Mass Transfer (DMT) can result in crack rebonding, and mechanical stiffness recovery. Crack rebonding driven by DMT occur wihin a few days at room temperature and low pressure. DMT is enhanced at higher temperatures, which could be beneficial for the sustainabilty of geological storage facilities in salt mines. On the one hand, visco-plastic laws relating creep microscopic processes to microstructure changes are empirical. On the other hand, theoretical models of damage and healing disconnect thermodynamic variables from their physical meaning. The proposed model enriches the framework of Continuum Damage Mechanics (CDM) with fabric descriptors. In order to infer the form of fabric tensors from microstructure observation, creep tests were carried out on granular salt under constant stress and humidity conditions.

Pictures: Zhu and Arson, 2014
Moments of probability of fabric descriptors are used to find relationships between microstructural and phenomenological variables. Creep processes in salt include glide, cross-slip, diffusion, and dynamic recrystallization. We assume that healing is predominantly governed by diffusive mass transfer. We model the corresponding crack cusp propagation on grain faces by means of a two-dimensional diffusion equation. We calibrate this grain-scale healing model against experimental measures of crack cusp propagation distance. We simulate the opening, closure and rebonding of three orthogonal families of micro-cracks during a compression-tension loading cycle. Multi-scale model predictions illustrate the evolution of stiffness, deformation, and crack geometry during the anisotropic damage and healing process, and highlight the increased healing efficiency with time. The proposed modeling approach is expected to provide more precise and reliable performance assessments on geological storage facilities in salt rock.
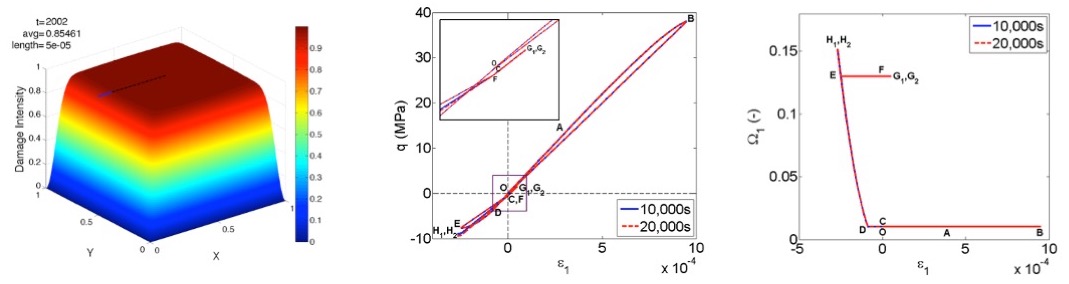
Pictures: Zhu and Arson, 2015